2013年04月26日
振り子スウィングの考察
相手ボールが速いとき
こちらも振り遅れないよう、小さく引くのは常識。
でも、今日は常識はずれの考察。
先日、朝の新聞を見たら、小学生の全国学力テスト問題が出ていた。
算数には私の大好物、振り子の問題が
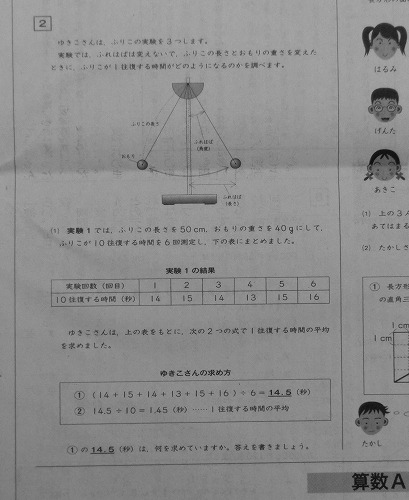
要は、振り子の支点からオモリまでの距離が一定なら
その振幅によらず、周期は一定になることの理解度を聞いている。
そりゃあ常識だ
俺がいつも言っているとおりだ、なんて思いながら、ふと ・・・
バックで、振幅が小さいと振り遅れないか?
バックハンドトップスピンで打点はかなり前

振り子の最下点より、時間的に後で打てば
どんな非力な人でも、アッパースウィングになる理屈。
もしもスウィングが小さめで
振幅がここまでいっていなければ
えっ、永久に届かない。
まあそこまで行かなくても
打点にやっと届くほどの振り子なら
最下点から打点までは
周期全体の4分の1の時間がかかる。
逆に振り幅を大きくすれば
全体の周期、端から端までの時間が一定なのだから
最下点から打点まではあっという間に到達する。
ここまでは小学生の算数、理科のレベルで理解できるのだ。
小学生レベルの結論は
構えが間に合うなら
大きく高いテイクバックのほうが
インパクトまでの時間が短く、間に合いやすいということ。

もちろんそのときのスウィング速度は
小さく引いた時よりもはるかに大きい。
定性的な考察なら小学生レベルで充分。
どうせ振り子以外の成分も入ってくるし ・・・
もしも、まじめな性格で、定量的に考えるなら?
ある大きさのスウィングで
インパクトまでの正確な時間と
そこでの速度を出すには
エネルギー保存の法則で
位置エネルギーを運動エネルギーに変換して ・・・
これは高校生レベルの力学で解けそう
微分、積分はいらない。
算数好き、物理好きの
ひまな人はチャレンジしてみてください。
もう一度、結論を。
振り子スウィングなら、大きく引いたほうが振り遅れない。
こちらも振り遅れないよう、小さく引くのは常識。
でも、今日は常識はずれの考察。
先日、朝の新聞を見たら、小学生の全国学力テスト問題が出ていた。
算数には私の大好物、振り子の問題が

要は、振り子の支点からオモリまでの距離が一定なら
その振幅によらず、周期は一定になることの理解度を聞いている。
そりゃあ常識だ
俺がいつも言っているとおりだ、なんて思いながら、ふと ・・・
バックで、振幅が小さいと振り遅れないか?
バックハンドトップスピンで打点はかなり前

振り子の最下点より、時間的に後で打てば
どんな非力な人でも、アッパースウィングになる理屈。
もしもスウィングが小さめで
振幅がここまでいっていなければ
えっ、永久に届かない。
まあそこまで行かなくても
打点にやっと届くほどの振り子なら
最下点から打点までは
周期全体の4分の1の時間がかかる。
逆に振り幅を大きくすれば
全体の周期、端から端までの時間が一定なのだから
最下点から打点まではあっという間に到達する。
ここまでは小学生の算数、理科のレベルで理解できるのだ。
小学生レベルの結論は
構えが間に合うなら
大きく高いテイクバックのほうが
インパクトまでの時間が短く、間に合いやすいということ。

もちろんそのときのスウィング速度は
小さく引いた時よりもはるかに大きい。
定性的な考察なら小学生レベルで充分。
どうせ振り子以外の成分も入ってくるし ・・・
もしも、まじめな性格で、定量的に考えるなら?
ある大きさのスウィングで
インパクトまでの正確な時間と
そこでの速度を出すには
エネルギー保存の法則で
位置エネルギーを運動エネルギーに変換して ・・・
これは高校生レベルの力学で解けそう
微分、積分はいらない。
算数好き、物理好きの
ひまな人はチャレンジしてみてください。
もう一度、結論を。
振り子スウィングなら、大きく引いたほうが振り遅れない。